Wells Fargo Campus Analytics Challenge Natural Language Processing

Repository with code.

Introduction

The main reasons for proposing an alternative framework is that tasks lacking labelled training data have largly remained unsolved in the realm of machine learning while tasks with immediately or cheaply collectable training labels have in the last decade seen tremendous progress. Topic modelling is one such example: it is an interdeciplinary sub-field between linguistics, statistical learning and computer science that tackles the problem of assigning related text of arbitrary length to a known or unknown number of topics.

Problem Statement

The main problems that make To topic modelling a challenging task are:

Data

Dataset information

The data provided by wells fargo for this tasks is a collections of meta-data for 24,395 datasets representing over 100 years of research by NASA. For the challege, only the dataset description can be used, and not its title. below is a list of fields in the dataset:

Field descriptions

Models

Below I briefly go into the theoretical basis of the models used in my solution for the contest.

Baseline Latent Dirichlet Allocation(LDA)

LDA is a generative probabilistics model used mostly in topic modelling. It does this by overlaying mixture distributions of topics over documents and by assuming all documents are made up of a finitly small set of repeating words over many documents. Its is typically implemented using dictionaries to keep track of word occurance counts and word co-occurance counts. The main problem with LDA to topic modelling is the need to specify the number of expected topics in the collection of doccuments, which is not always known. The second problem with LDA is that it only considers word occurance counts and not word co-occurance possitions, which do play a role in the overall understanding of the documents hence more robust topics.

Proposed solution

To addres the issues detailed in the problem statement, this work proposes as a solution, a framework for applying machine learning mostly used in the physical sciences. In most physical sciences such as astronomy, physics and biology, methods with known theoretical backing for solving problems are know(the phenominon is understood scientifically), however, the accepted solution is sometimes too computationally demanding or expensive. sometimes, simulations can be run, however, the underlying phenomenon is too complex to formulate mathematically. In both cases, neural networks(which are universal function approximators) have been used to approximate the underlying phenomenon. Borrowing from this idea and recalling I recently learned from my network science class how to perform hierachical overlapping clustering using link community detection algorithms on graphs.

The combination of these two ideas lead me to proposing: using machine learning to approximate a known network science algorithm. In this solution, a completely unsupervised classical network science algorithm’s results is used as a way for providing “true labels” to a multi-label machine learning task. this means we are transforming unsupervised topic modelling into “sudo supervised” learning by approximating hierachical link community detection.

Limitations

Data pipeline for framework

The flow diagram below is a summary of the flow of data in the proposed solution. The blue arrows represent traininf process and the dotted grey represent inference steps.

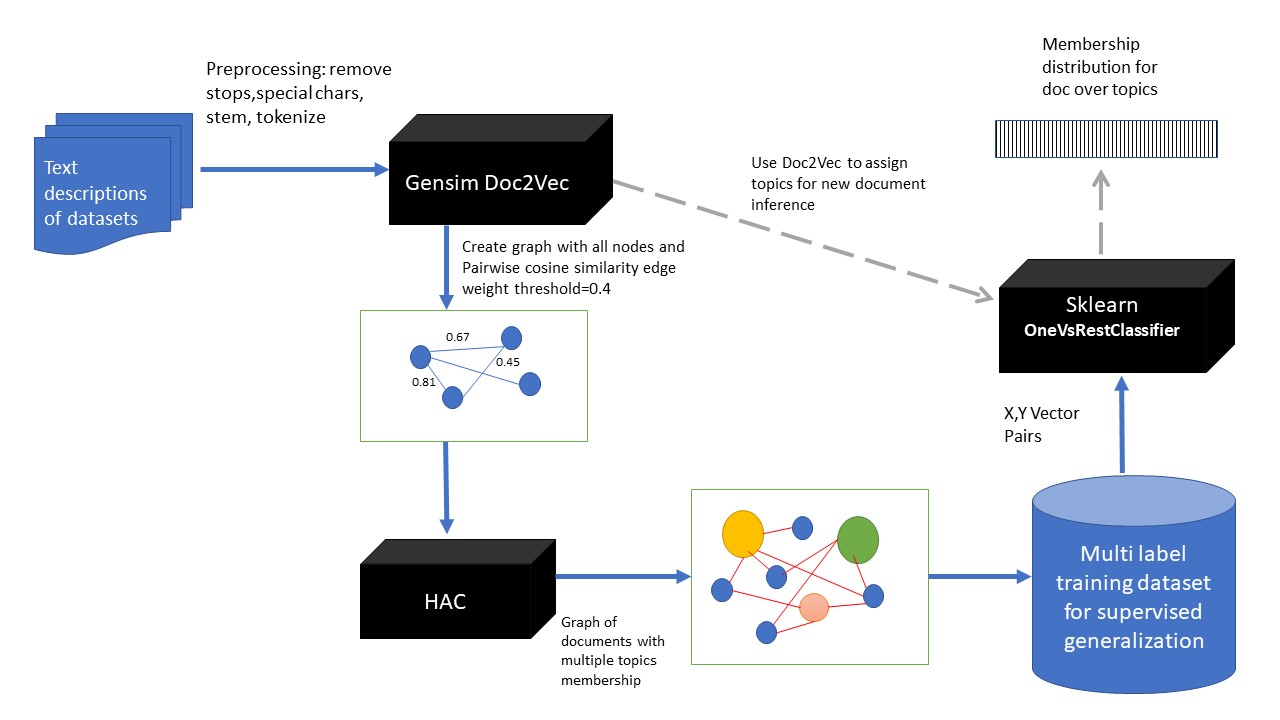
Doc2Vec

Doc2vec, like word2vec, are set of algorithms for extracting vector representations of documents by training a shallow neural network in a manner that preserves meaning. document vector representation are trained as en extension to the manner in which word vectores are trained, instead of only using context words in predicting centre word, a document vector embeding is also trained by using each document’s unique ID as input too. In a way it acts as memory for context of words in each document.

This model is espeacially versatile since it trains document level vectors by leveraging skip-gram word vectors and so is able to infer a document vector for documents that are not in the training dataset at all.

In hierachical Agglomerative clustering (HAC), clusters are resursively formed by merging pairs of point in a Bottom-up manner to form clusters that maximizes a predefined distance measure between clusters. There are 4 types of cluster distance measures namely single linkage, average linkage, ward, and complete linkage.